[ICML 2025] GuidedQuant

Overview - GuidedQuant
GuidedQuant is a post-training quantization (PTQ) framework that compresses large language models while retaining accuracy. It improves on two dominant PTQ approaches:
1. Layer-wise Output-based Quantization: Minimizes the mean-squared error between each layer's original and quantized outputs, but treats all hidden features equally and thus ignores how much each feature matters to the end loss.
\[ \| \mathbf{X}^{(l)} {\mathbf{W}}^{(l)} - \mathbf{X}^{(l)} \widehat{\mathbf{W}}^{(l)}\|_F^2 = \sum_{i=1}^n \sum_{j=1}^{d_\mathrm{out}^{(l)}} \left(Z_{ij}^{(l)} - \widehat{Z}_{ij}^{(l)} \right)^2 \]2. Diagonal-Fisher Methods: Weight errors by gradients of the end loss, yet approximate the Hessian with only its diagonal, discarding crucial cross–weight interactions.
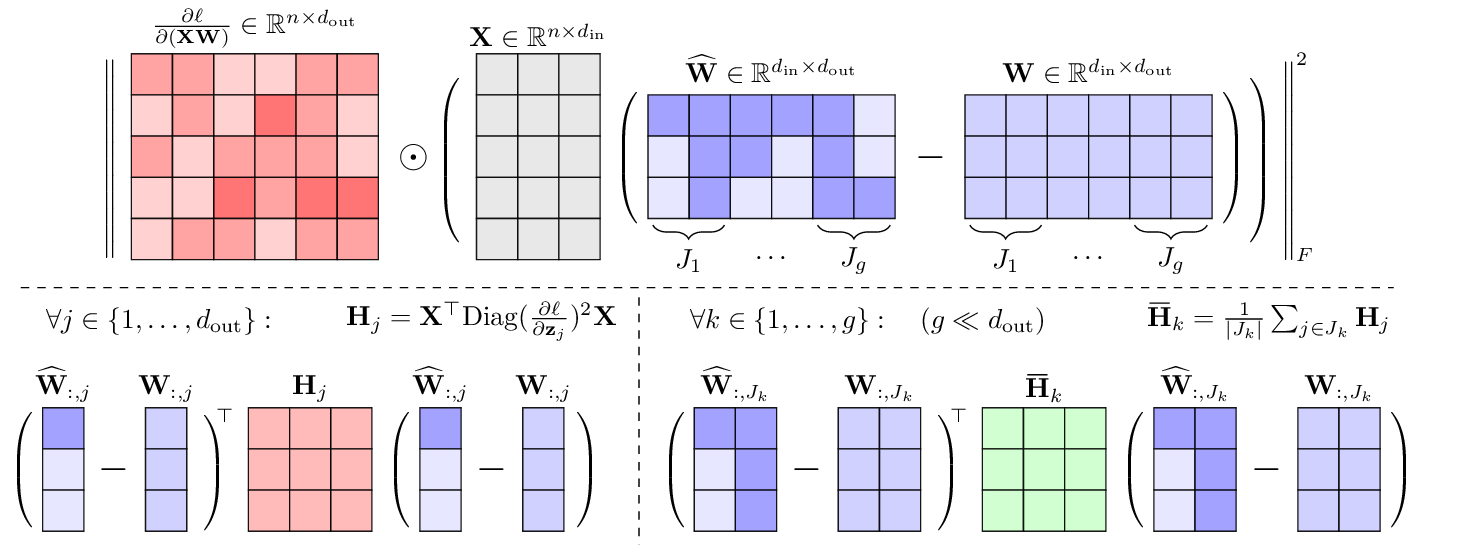
\[(\widehat{\mathbf{w}} - \mathbf{w})^\top \mathrm{diag}(\mathbf{F}) (\widehat{\mathbf{w}} - \mathbf{w}) = \sum_k F_{kk} (\widehat{w}_k - w_k)^2\]GuidedQuant bridges these gaps by integrating end loss gradients into the quantization objective while preserving intra-channel dependencies. \begin{align} & \left\lVert \color{blue}{\frac{\partial \ell}{\partial \mathbf{Z}^{(l)}} \odot} (\mathbf{X}^{(l)} {\mathbf{W}}^{(l)} - \mathbf{X}^{(l)} \widehat{\mathbf{W}}^{(l)}) \right\rVert_F^2 \nonumber \\ = n \sum_{l=1}^L &\sum_{j=1}^{d_\mathrm{out}^{(l)}} (\mathbf{w}^{(l)}_j - \widehat{\mathbf{w}}^{(l)}_j)^\top \color{blue}{\mathbf{F}^{(l)}_j} (\mathbf{w}^{(l)}_j - \widehat{\mathbf{w}}^{(l)}_j). \end{align} This objective corresponds to block-diagonal Fisher information approximation, and we make it scalable by grouping the Fisher blocks and averaging them within each group. The resulting objective can be plugged into any layer-wise PTQ backend, and improves state-of-the-art weight-only scalar, weight-only vector, and weight-and-activation quantization methods.
Overview - LNQ
For non-uniform scalar quantization, the optimization problem involves discrete assignment $\mathbf{P}^{(j)} \in \{0, 1\}^{d_\mathrm{in} \times m}$ and continuous codebook $\mathbf{c}^{(j)} \in \mathbb{R}^m$: \begin{align} \underset{\substack{\mathbf{P}^{(j)} \in \{0, 1\}^{d_\mathrm{in} \times m} \\ \mathbf{c}^{(j)} \in \mathbb{R}^m}}{\mathrm{minimize}}\;\; &\sum_{j=1}^{d_{\mathrm{out}}}\| \mathbf{X}\mathbf{w}_j - \mathbf{X}\mathbf{P}^{(j)}\mathbf{c}^{(j)} \|_2^2 \nonumber \\ \mathrm{subject\;to\;}~~~ &\mathbf{P}^{(j)}\mathbf{1}_m = \mathbf{1}_{d_\mathrm{in}}. \end{align} We further introduce Layer-wise Non-uniform Quantization (LNQ): an alternating optimization method with a closed-form codebook update and a coordinate-descent assignment update, giving a provable descent property. \begin{align} &\textbf{repeat:} \\ &\quad \mathbf{c}^{(j)} \leftarrow \left(\mathbf{P}^{(j)}{}^\top \mathbf{X}^\top \mathbf{X} \mathbf{P}^{(j)}\right)^{-1}\mathbf{P}^{(j)}{}^\top \mathbf{X}^\top \mathbf{X} \mathbf{w}_j \quad \quad \color{blue}{\text{(codebook)}}\\ \end{align} \begin{align} &\quad \textbf{for}~~ i=1 ~~\textbf{to} ~~ d_\mathrm{in} ~~ \textbf{do:}\\ &\quad \quad c^{(j)}_{q^*} \!\! \leftarrow \!\!\!\!\underset{\widehat{W}_{ij} \in \{c_1^{(j)}, \ldots, c_m^{(j)}\}}{\mathrm{argmin}} \!\!\!\! (\widehat{\mathbf{w}}_j \!-\! \mathbf{w}_j)^\top \mathbf{X}^\top \mathbf{X} (\widehat{\mathbf{w}}_j \!-\! \mathbf{w}_j) \\ &\quad \quad \forall q\in [m]: P^{(j)}_{iq} = \begin{cases} 1 & \text{if } q = q^*, \\ 0 & \text{otherwise.} \end{cases} ~~~~~~~~~~ \color{blue}{\text{(assignment)}} \end{align} Combined with GuidedQuant, LNQ significantly outperforms SqueezeLLM in perplexity while using the same CUDA kernel (e.g., 2-bit Llama-2-7B : 39.6 → 8.8).
Summarized Results
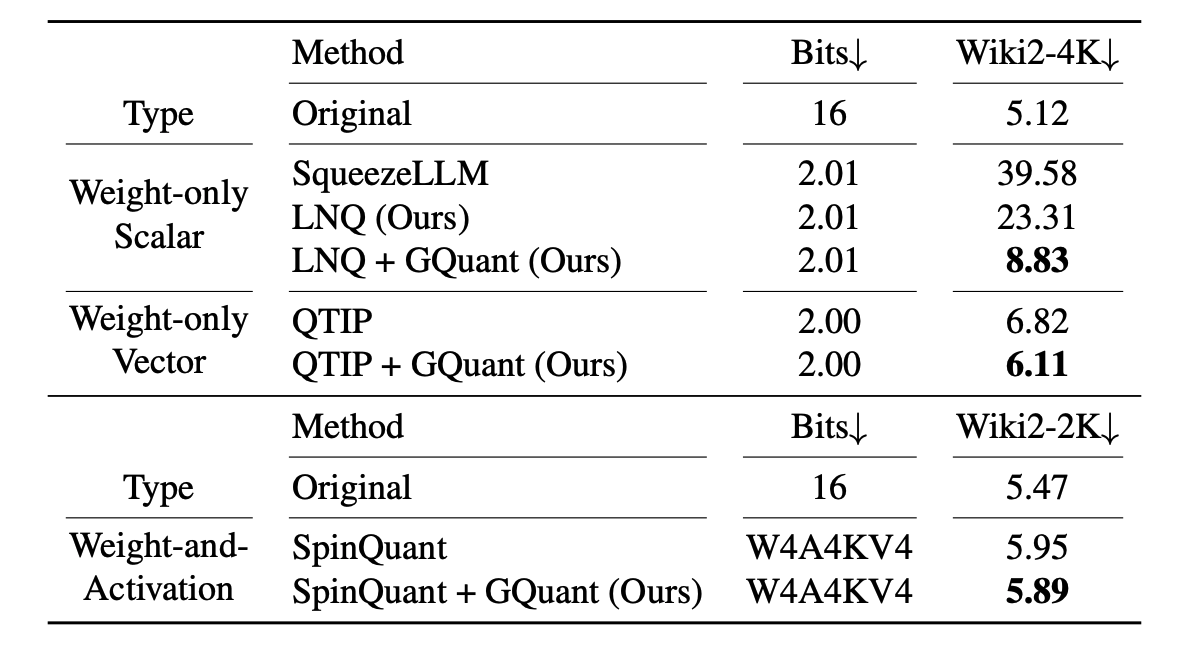
We present the summarized results of applying GuidedQuant to state-of-the-art PTQ methods on the Llama-2-7B model. Evaluation on the WikiText2 dataset with context lengths of 4096 (Wiki2-4K) and 2048 (Wiki2-2K) shows that GuidedQuant consistently improves perplexity across all PTQ methods.
BibTeX
@inproceedings{kim2025guidedquant,
title={GuidedQuant: Large Language Model Quantization via Exploiting End Loss Guidance},
author={Jinuk Kim and Marwa El Halabi and Wonpyo Park and Clemens JS Schaefer and Deokjae Lee and Yeonhong Park and Jae W. Lee and Hyun Oh Song},
booktitle = {International Conference on Machine Learning (ICML)},
year={2025},
}