TL;DR We propose a subset selection problem that replaces inefficient activation layers with identity functions and optimally merges consecutive convolution operations into shallow equivalent convolution operations for efficient inference latency.

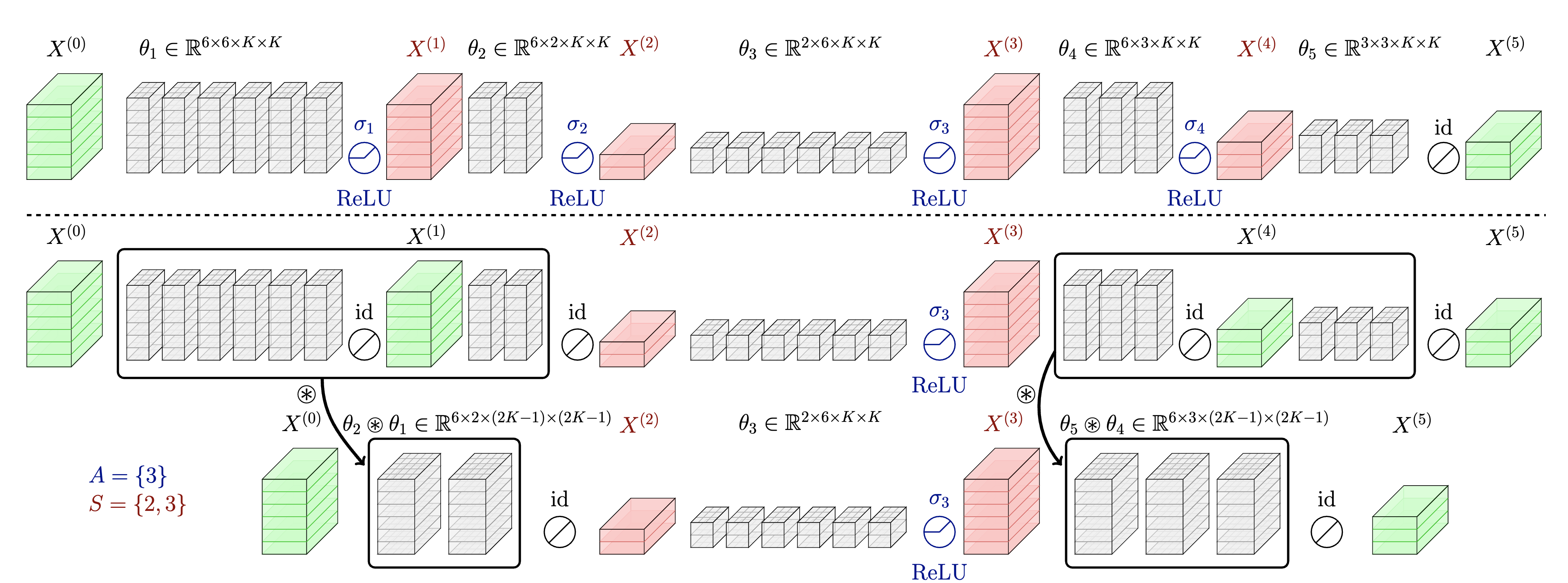
cmp gif

An illustration of depth compression for a five-layer CNN.

Preliminary

In the realm of real-world deployment of neural networks, two paramount considerations come to the forefront. First, the network must be able to attain a sufficiently high accuracy. Secondly, it is imperative that the network exhibits minimal latency and low run-time memory.

Motivation

Motivation for this research stems from the idea that consecutive convolutional layers without the activation layers in between can be merged into an single convolutional layer because of the associative property of the convolution operation.

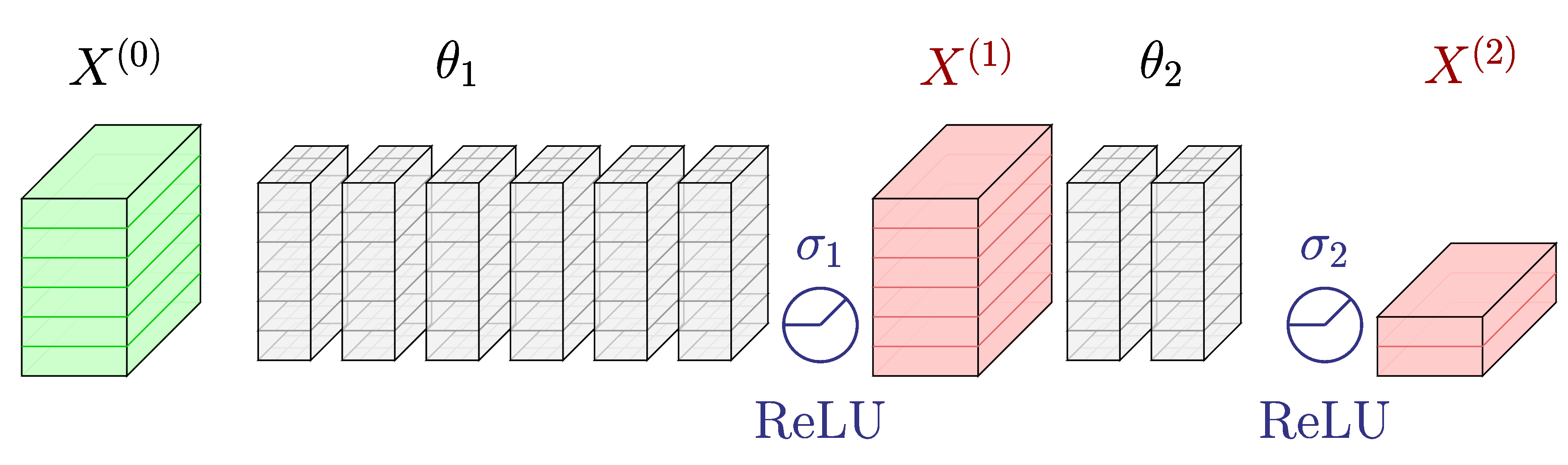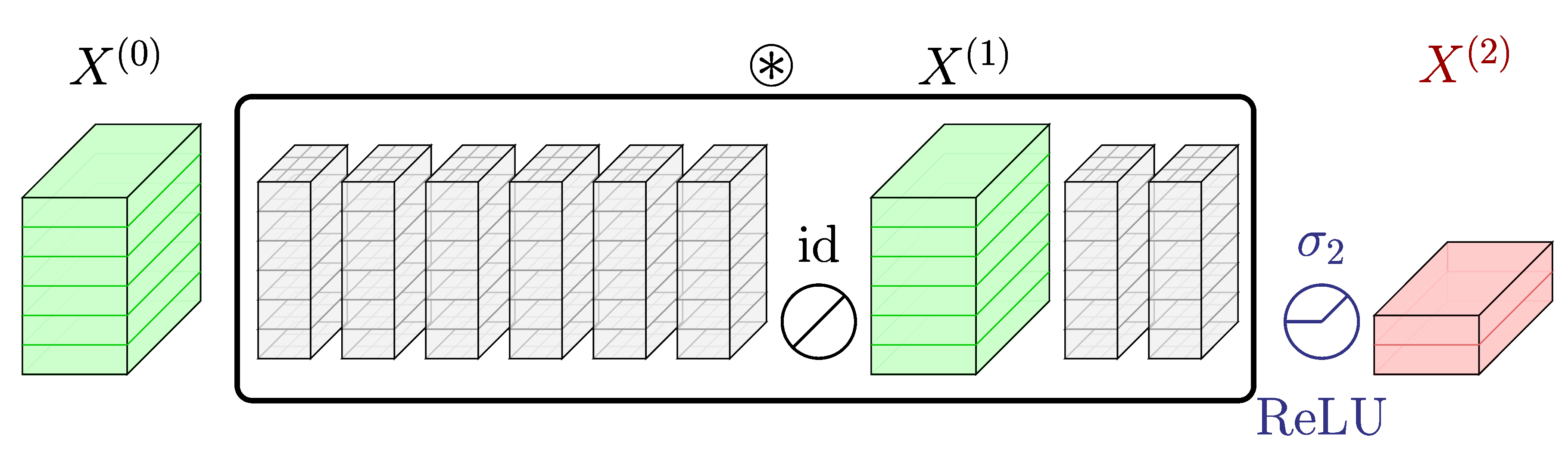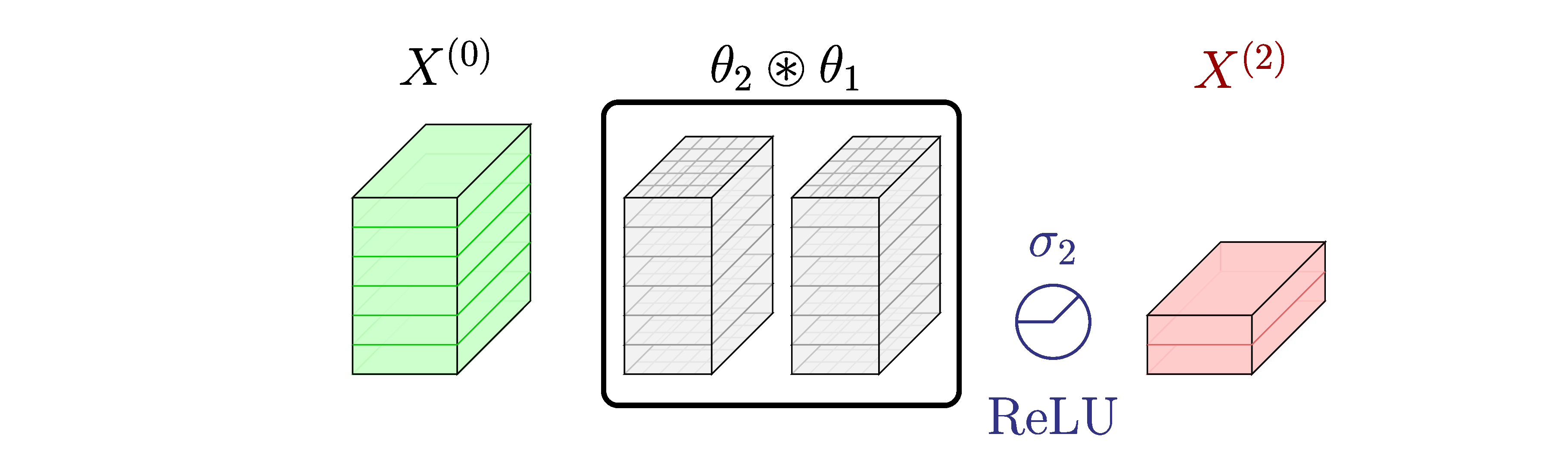
cmp gif

An illustration of merging two consecutive convolutional layers into a single layer.

Consequently, by eliminating unnecessary activation layers and compressing the depth of the CNN, we can drastically reduce run-time memory and improve inference latency.

Notation

  • Convolution parameter: $\theta_l \in \mathbb{R}^{C_{l-1} \times C_l \times K_l \times K_l}$.
  • Activation layer: $\sigma_l$.
  • Convolution operation: not1
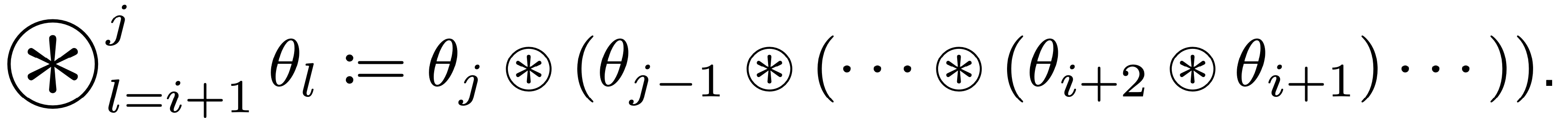
  • Function composition: not1
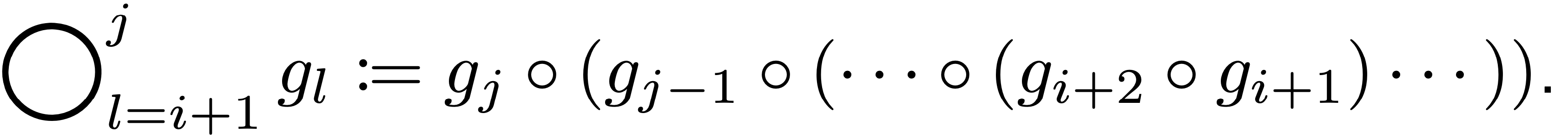
  • CNN Network ($L$-layer): not1

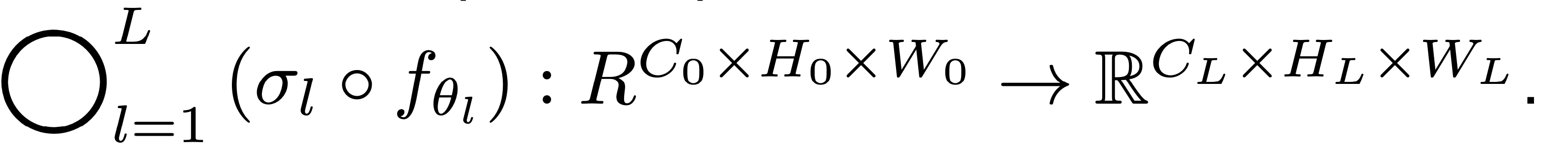
Goal

Driven by our motivation, our principal research objectives are twofold.

  • Firstly, our primary goal is to optimize the replacement of a subset of activation layers with an identity function.
  • Secondly, we endeavor to minimize the latency of the resultant network while preserving its performance.

Methods

Optimal subset selection for depth compression

We first introduce set $A = \{ a_i \}$ to represent the layer indices where the activation layer is kept intact. Our objective is to enhance the network’s accuracy by replacing activation layers based on the set $A$, while staying within the latency constraints of the merged network. This is formulated as follows:

not1

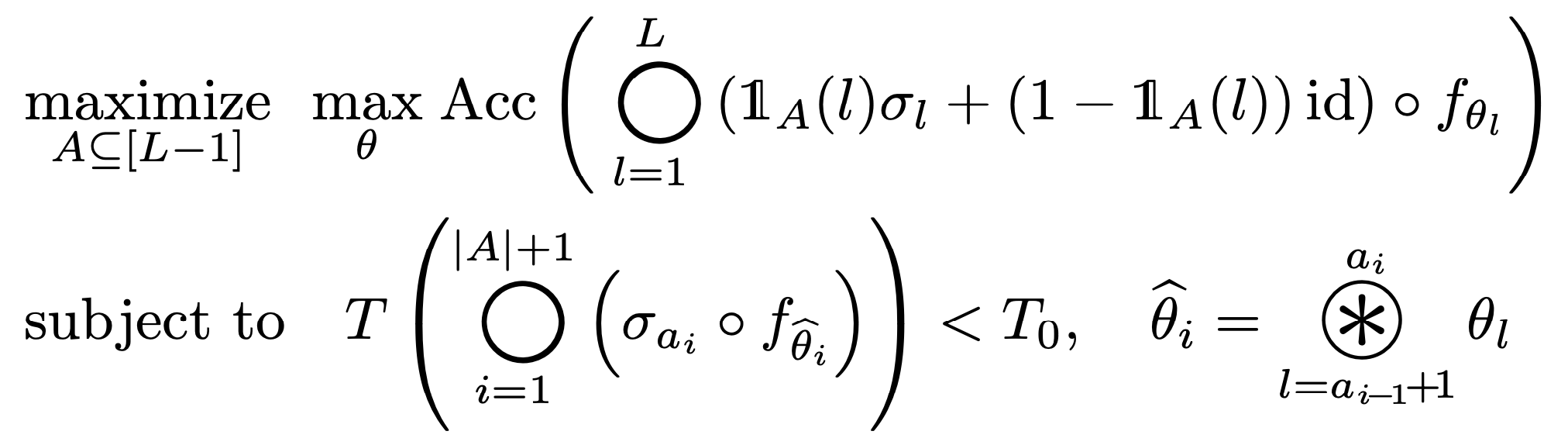
An optimal subset selection problem for depth compression (initial form).

Initially, we present a simplified version of our ultimate optimization problem. In this formulation, we merge all convolutional layers located between the activated indices. Subsequently, we will expand on this formulation by introducing set $S = \{ s_i \}$ to govern the merging pattern.

Latency constraint

With regard to the latency constraint, we assess the inference latency of the merged network by adding up the latencies of each merged layer.

eq2

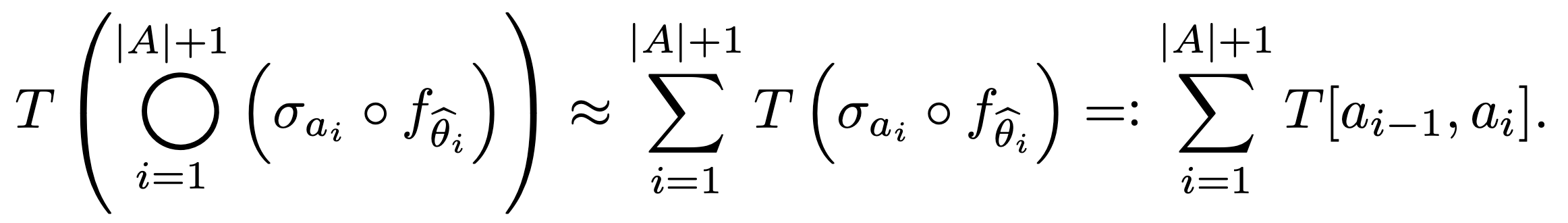
Here, we define $T[i, j] := T(f_{\theta’})$ where 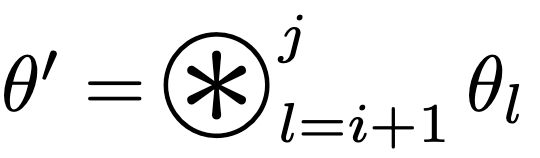ineq1 (merging the layers from $i+1$ to $j$).

Surrogate objective

In order to optimize the network performance, we take note of the fact that our set $A$ partitions the network into contiguous network blocks, 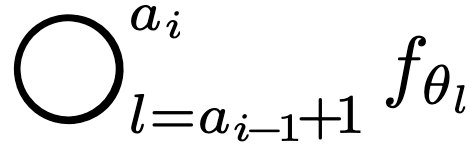ineq2, which has activation layers at the boundaries.

eq3

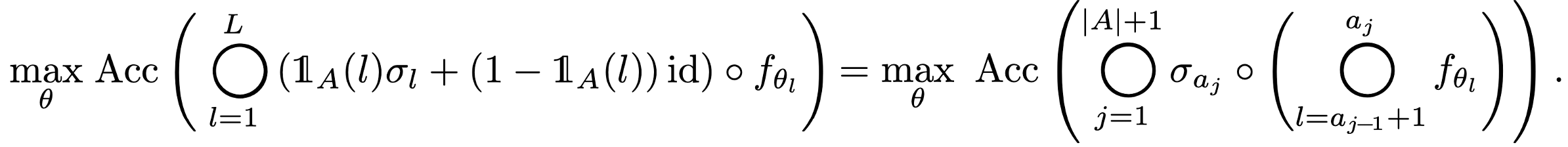
Nevertheless, estimating the accuracy for every possible combination of these network blocks is not feasible.

To resolve this, we propose using the sum of the importance of each sub-block as the surrogate objective, as shown in the following equation:

eq4

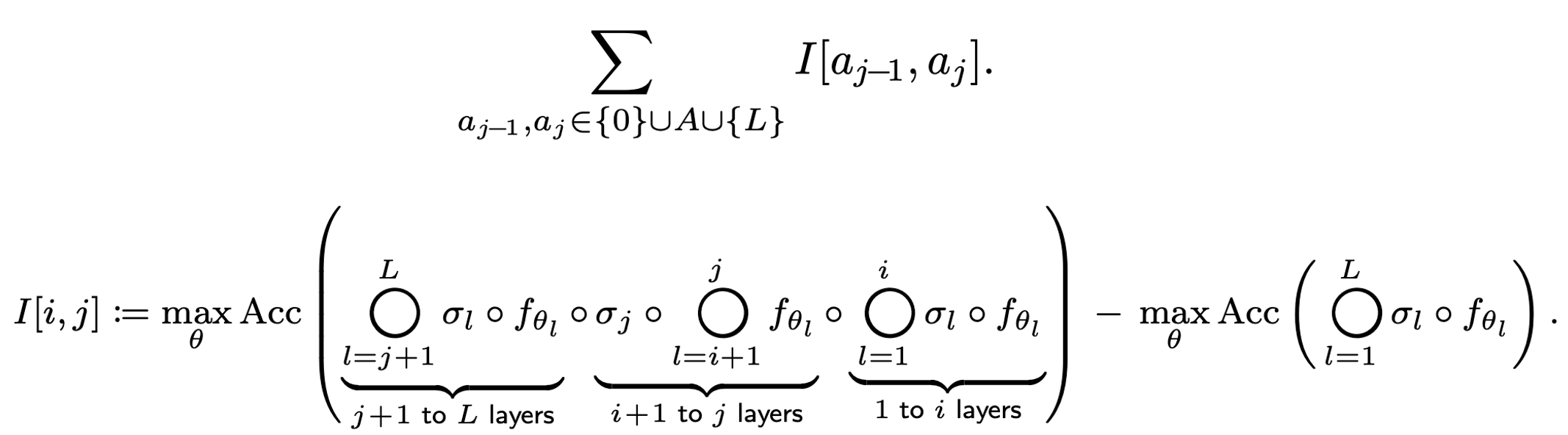
For the importance value, we define it to be the negative accuracy drop when we deactivate the activation layers between the $i+1$-th and $j$-th layers in the original network. Consequently, a greater decrease in accuracy caused by the sub-block results in a smaller assigned importance value.

Optimization with dynamic programming

Now that we have defined our surrogate objective, we can reformulate our optimization problem as follows:

eq5

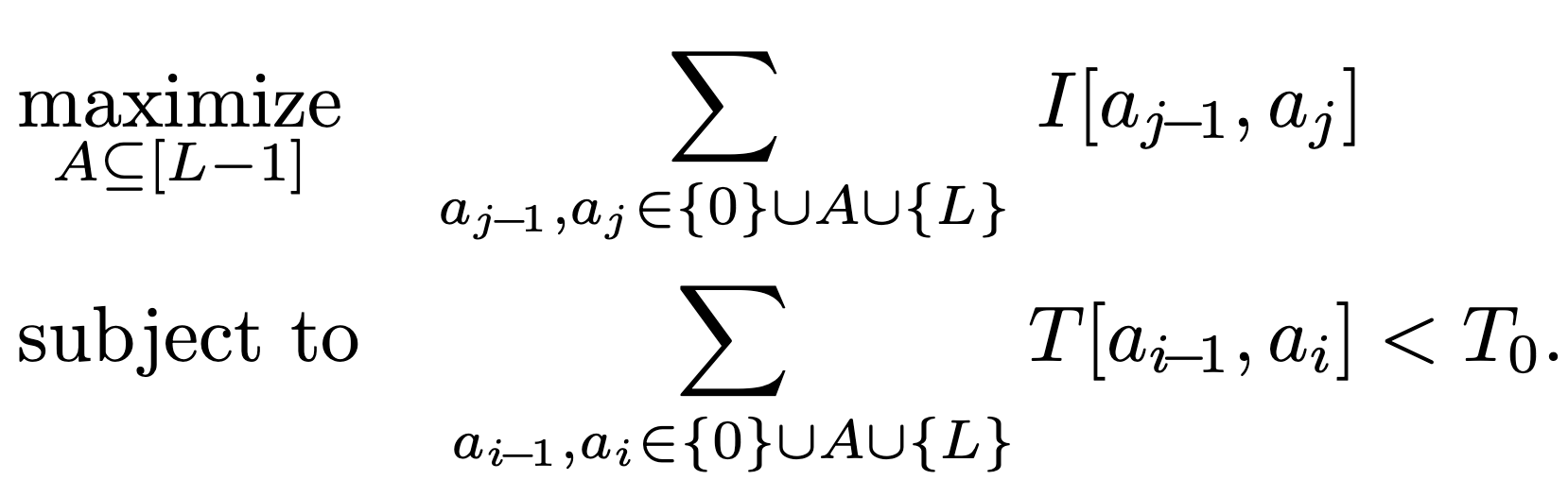
Here, we are trying to maximize the sum of importances while adhering to latency constraints.

Once we reformulate our problem with the surrogate objective, we can find the exact solution via dynamic programming with the following recurrence relation:

eq6

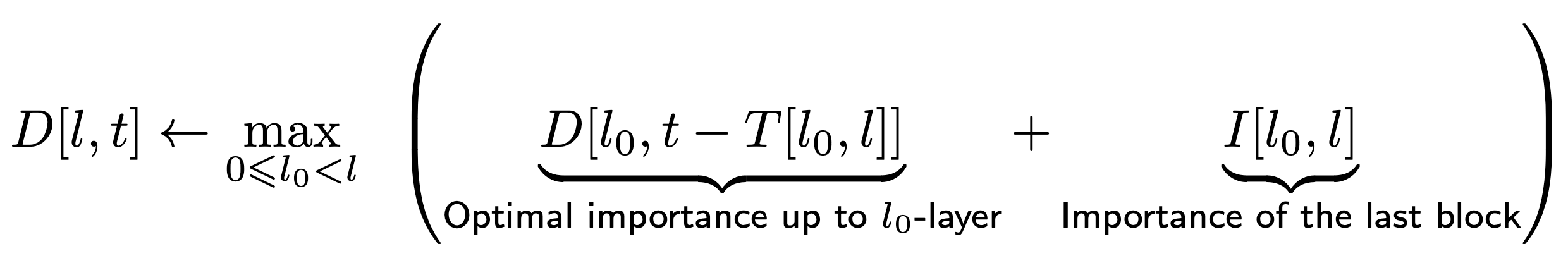
The recurrence relation involves the variable $D[l, t]$, denoting the maximum value for the sub-optimization problem associated with network compression up to the $l$-th layer while adhering to the specified latency budget $t$.

Pitfall: Not every merging helps!

However, it’s crucial to remember that not every merging operation contributes to improved efficiency. For example, if the number of intermediate channels are smaller than the first and the last channel, it might lead to a larger merged convolutional layer. Therefore, it’s important to be selective when we merge the network to obtain faster latency.

To address this issue, we introduce a new set, $S$, into our formulation. Set $S$ denotes the layer indices where we choose not to merge, providing us with another level of granularity in optimizing our network. Concretely, our objective is reformulated as follows:

eq7

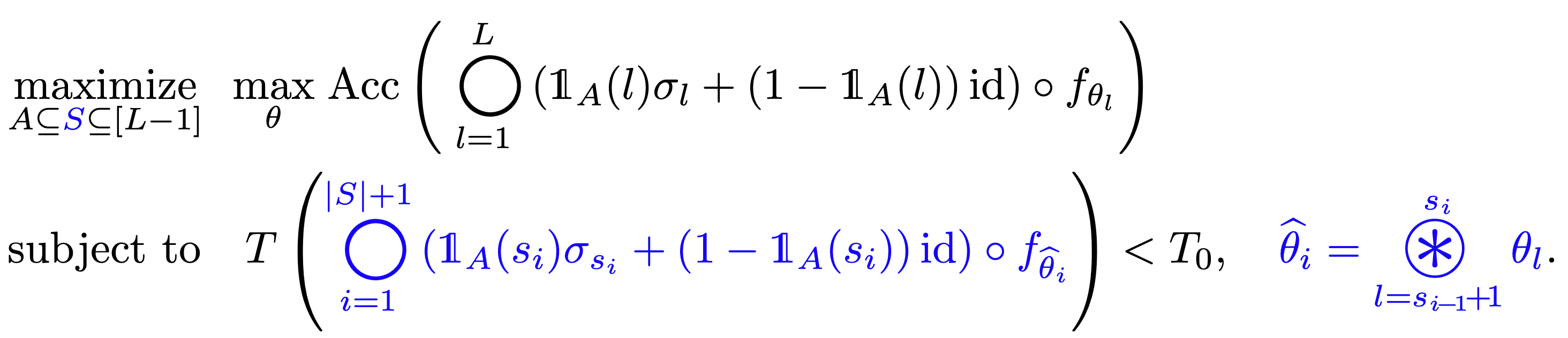
An optimal subset selection problem for depth compression
(the blue part represents the difference from the initial form).

It’s important to note that set $A$, representing layer indices where the activation layer is kept intact, is a subset of set $S$. The revised objective and the constraint are shown above, and the difference is that we merge according to the elements of set $S$ instead of set $A$.

With this new formulation that includes set $S$, we redefine our optimization problem, still maintaining our original goal: maximizing the sum of importances, subject to the latency constraint. However, this time, our latency constraint involves the summation over the elements of set $S$.

eq8

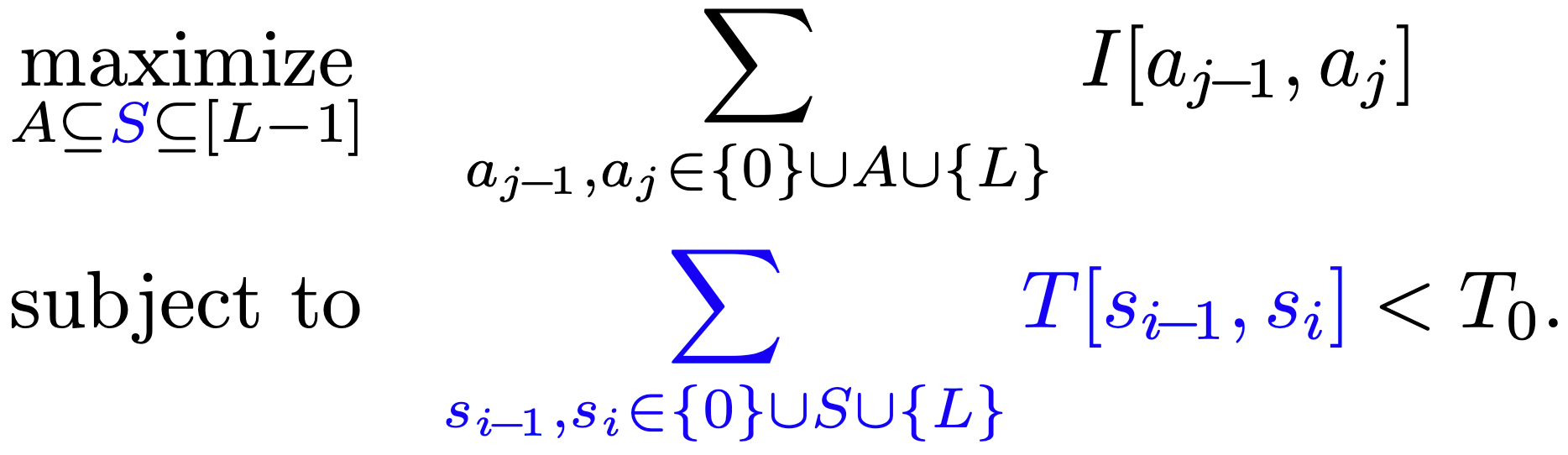
Similar to our previous approach, we can use dynamic programming to solve this new optimization problem. The recurring relation still stands, but with an updated definition of $T_{\text{opt}}$ to address to the inclusion of set $S$ in our formulation. The recurrence relation is as follows:

eq9

Here, we can obtain the table $T_{\text{opt}}$ through the dynamic programming.

Summary

Dynamic programming algorithm

In summary, we solve our proposed optimization problem, which is to maximize the sum of importances subject to the latency constraint, using a two-stage dynamic programming approach.

  1. At the first stage, we obtain table $T_{\text{opt}}$ using dynamic programming.
  2. At the second stage, we obtain the maximum importance $D[l, t]$ and the optimal solution ($A[l, t]$, $S[l, t]$) using the dynamic programming recurrence relation.

To improve performance in MobileNetV2, we introduce the sub-blocks that have non-linear activation layers in the places where original network doesn’t have one. Then, we further tailor the optimization problem to incorporate these blocks. For the details, refer to the Appendix B in the original paper.

Overall process

The overall process of our method can be summarized as follows:

  1. Measure the time ($T$) and importance ($I$) for possible network blocks.
  2. Solve the DP recurrence to obtain the optimal set $A$ and $S$.
  3. Replace the activation layers not present in $A$ with identity functions, then finetune the network until convergence.
  4. At the test time, merge the finetuned network following $S$ and evaluate the latency.

Experimental results

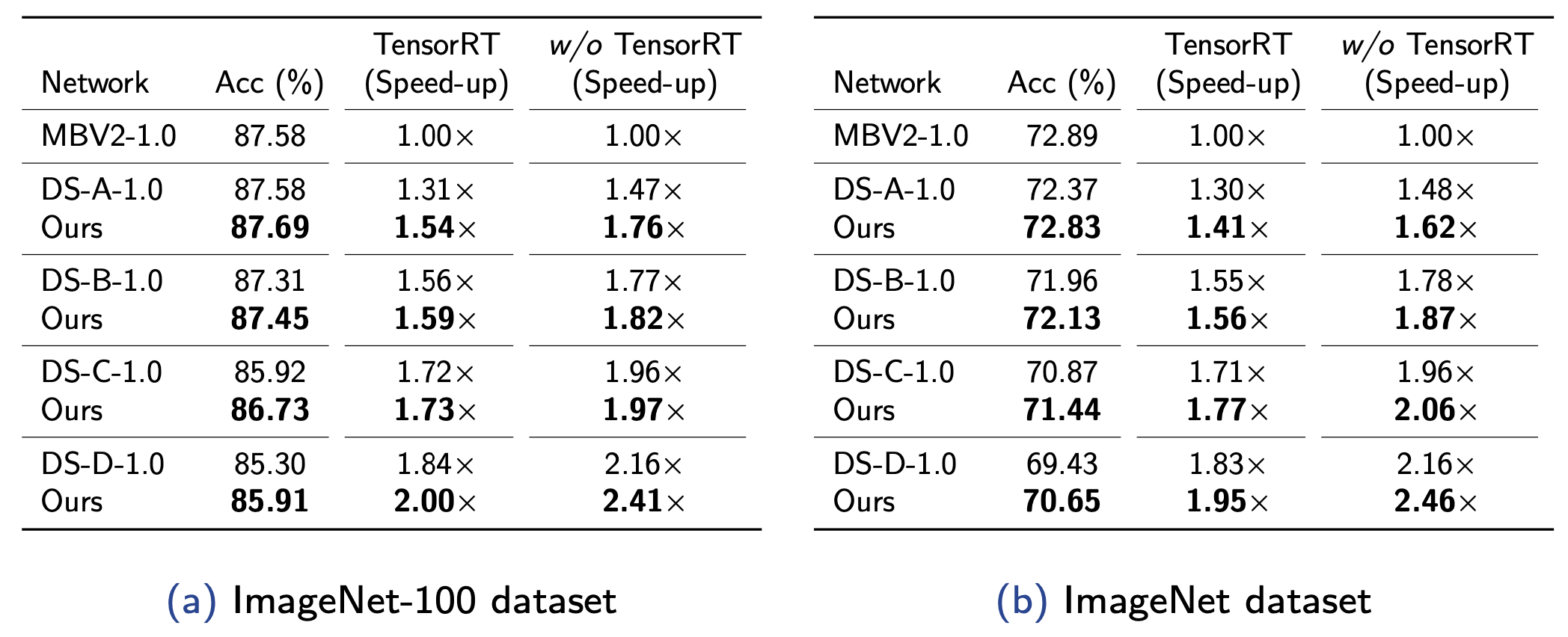
table1

Accuracy and latency of compressed architectures applied to MobileNetV2-1.0.

In our experiments, we applied our compression method to MobileNetV2 and evaluate on the ImageNet dataset. Notably, our method achieves state-of-the-art performance, 1.54$\times$ speed-up without losing any accuracy in ImageNet-100 dataset, and achieve 1.41$\times$ speed-up with very modest accuracy drop in ImageNet dataset.

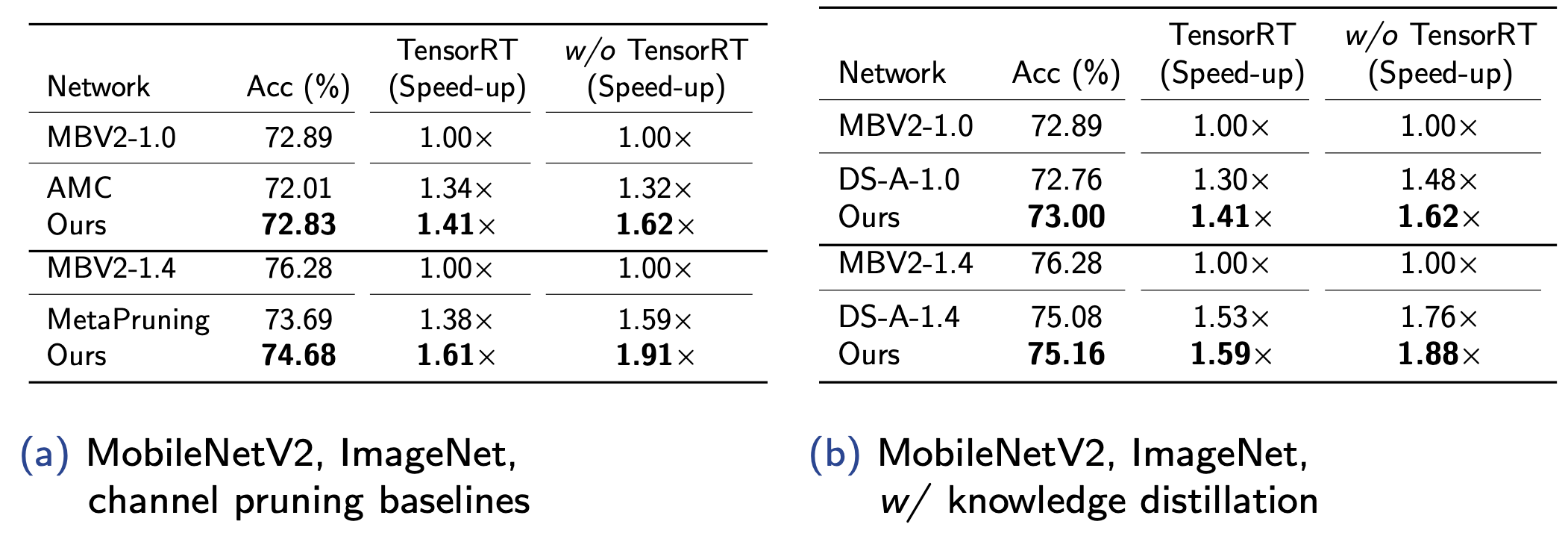
table2

Accuracy and latency of compressed architectures applied to MobileNetV2.

We further present the results of comparing with the channel pruning baselines and adopting the knowledge distillation from the pre-trained weights. Our method achieves 1.41$\times$ speed-up without losing any accuracy in the ImageNet dataset with the knowledge distillation.

Citation

@inproceedings{kim2023efficient,
    title={Efficient Latency-Aware CNN Depth Compression via Two-Stage Dynamic Programming}, 
    author={Kim, Jinuk and Jeong, Yeonwoo and Lee, Deokjae and Song, Hyun Oh},
    booktitle = {International Conference on Machine Learning (ICML)},
    year={2023}
}